[Algorithm] C++ 백준 1005번 : ACM Craft

ACM Craft 문제는 여러 건물을 짓기 위해 주어진 순서와 시간을 고려하여 특정 건물을 완성하는 데 필요한 최소 시간을 계산하는 문제이다. 각 건물은 다른 건물들이 완성된 후에야 지을 수 있으며, 주어진 건설 순서 규칙에 따라 건물들 간의 의존 관계가 형성된다. 목표는 주어진 입력 데이터에 따라 최종적으로 특정 건물을 완성하는 데 걸리는 최소 시간을 구하는 것이다. 이를 위해 위상 정렬과 동적 계획법을 사용하여 효율적으로 문제를 해결해야 한다.

문제 원문

문제 설명

여러 건물을 짓는 데 걸리는 시간이 주어지고, 특정 건물을 짓기 위해 다른 건물들이 먼저 지어져야 하는 순서 관계가 있다. 목표는 특정 건물을 짓기까지 걸리는 최소 시간을 계산하는 것이다.

각 건물은 특정 시간 동안 지어야 하며, 어떤 건물을 짓기 위해서는 그 전에 다른 건물들이 먼저 지어져야 한다.
여러 테스트 케이스가 주어지며, 각 테스트 케이스마다 다음과 같은 정보가 주어진다:
1. 건물의 수 \(N\)과 건설 순서 규칙의 수 \(K\).
2. 각 건물의 건설 시간.
3. \(K\)개의 건설 순서 규칙.
4. 목표 건물의 번호.


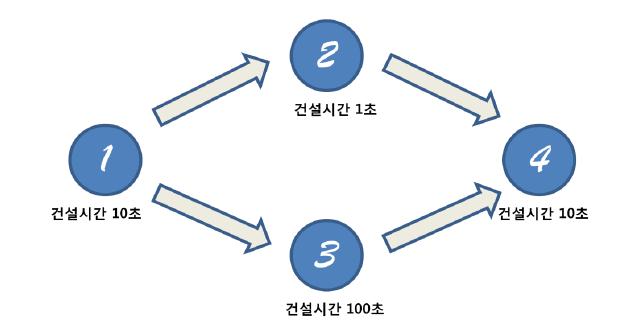이미지로 형상화

입력:

테스트 케이스의 수.
각 테스트 케이스:
- 건물의 수 \( N \)과 규칙의 수 \( K \).
- 각 건물을 짓는 데 걸리는 시간.
- 건설 순서 규칙.
- 최종적으로 건설해야 하는 건물 번호.

출력:

각 테스트 케이스마다 최종적으로 건설해야 하는 건물을 짓기까지 걸리는 최소 시간을 출력한다.

예제:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
2
4 4
10 1 100 10
1 2
1 3
2 4
3 4
4
8 8
10 20 1 5 8 7 1 43
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7
7

출력:

해결 방법

위상 정렬을 사용하여 각 건물의 건설 순서를 결정한다.
동적 계획법을 사용하여 각 건물을 짓기 위한 최소 시간을 계산한다.

알고리즘

각 건물의 선행 조건을 그래프로 표현하고 위상 정렬을 수행한다.
각 건물에 대해 동적 계획법을 사용하여 필요한 최소 시간을 계산한다.

이 문제를 해결하기 위해선 위상 정렬(Topological Sorting)과 동적 계획법(Dynamic Programming)을 사용하여, 각 건물을 짓는 데 필요한 최소 시간을 계산해야 한다.

아래는 이를 해결하기 위한 Python 코드를 작성한 예시이다:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from collections import deque

def find_build_time(N, K, build_times, rules, target):
    in_degree = [0] * (N + 1)
    graph = [[] for _ in range(N + 1)]
    dp = [0] * (N + 1)
    
    for x, y in rules:
        graph[x].append(y)
        in_degree[y] += 1
    
    queue = deque()
    for i in range(1, N + 1):
        if in_degree[i] == 0:
            queue.append(i)
            dp[i] = build_times[i-1]
    
    while queue:
        current = queue.popleft()
        for neighbor in graph[current]:
            in_degree[neighbor] -= 1
            dp[neighbor] = max(dp[neighbor], dp[current] + build_times[neighbor-1])
            if in_degree[neighbor] == 0:
                queue.append(neighbor)
    
    return dp[target]

def main():
    T = int(input())
    for _ in range(T):
        N, K = map(int, input().split())
        build_times = list(map(int, input().split()))
        rules = [tuple(map(int, input().split())) for _ in range(K)]
        target = int(input())
        print(find_build_time(N, K, build_times, rules, target))

if __name__ == "__main__":
    main()

위 코드는 시간 초과가 발생한다. 따라서, 시간 초과 문제를 해결하기 위해 알고리즘을 최적화할 필요가 있다. 주어진 문제는 위상 정렬을 사용하여 건물을 짓는 데 필요한 최소 시간을 계산하는 문제이다. 현재 코드에서 시간을 줄일 수 있는 부분들에 대해 분석해 보자.

입력 처리 방식 최적화:
- 현재 입력을 input()으로 한 줄씩 처리하고 있다. 이는 입력이 많을 때 비효율적이다. sys.stdin.read()를 사용하여 한 번에 입력을 받아오면 I/O 시간을 크게 줄일 수 있다.
중복된 계산 제거:
- 각 건물의 최소 건설 시간을 dp 배열에 저장하여, 이미 계산된 값이 있다면 다시 계산하지 않고 재사용한다. 이 부분은 잘 구현되어 있어 중복 계산을 피하고 있다.
위상 정렬의 효율성:
- deque를 사용하여 큐 연산을 효율적으로 처리하고 있다. 위상 정렬 자체는 O(N + K)로 효율적이므로, 이 부분은 더 최적화할 필요는 없다.
전체 알고리즘 최적화:
- 위상 정렬을 사용하여 그래프를 한 번만 순회하고, 각 건물의 건설 시간을 한 번씩 계산하는 구조로, 이미 최적화된 상태이다.
불필요한 리스트 복사 최소화:
- 큰 입력 데이터를 다룰 때, 불필요한 리스트 복사는 피하는 것이 좋다. 예를 들어, build_times 리스트에서 값을 가져올 때 인덱싱을 사용하므로, 리스트 복사가 발생하지 않는다.

아래는 시간 복잡도를 줄이기 위해 더 효율적인 코드를 작성한 것이다.

최적화된 코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from collections import deque
import sys
input = sys.stdin.read

def find_build_time(N, K, build_times, rules, target):
    in_degree = [0] * (N + 1)
    graph = [[] for _ in range(N + 1)]
    dp = [0] * (N + 1)
    
    for x, y in rules:
        graph[x].append(y)
        in_degree[y] += 1
    
    queue = deque()
    for i in range(1, N + 1):
        if in_degree[i] == 0:
            queue.append(i)
            dp[i] = build_times[i-1]
    
    while queue:
        current = queue.popleft()
        for neighbor in graph[current]:
            in_degree[neighbor] -= 1
            dp[neighbor] = max(dp[neighbor], dp[current] + build_times[neighbor-1])
            if in_degree[neighbor] == 0:
                queue.append(neighbor)
    
    return dp[target]

def main():
    data = input().split()
    idx = 0
    T = int(data[idx])
    idx += 1
    results = []
    for _ in range(T):
        N = int(data[idx])
        K = int(data[idx + 1])
        idx += 2
        build_times = list(map(int, data[idx:idx + N]))
        idx += N
        rules = [tuple(map(int, data[idx + i * 2:idx + i * 2 + 2])) for i in range(K)]
        idx += 2 * K
        target = int(data[idx])
        idx += 1
        results.append(find_build_time(N, K, build_times, rules, target))
    
    for result in results:
        print(result)

if __name__ == "__main__":
    main()

이 코드는 sys.stdin.read를 사용하여 입력을 한 번에 읽어들이고, 입력 데이터를 파싱하여 처리하는 방식을 사용하였다. 이를 통해 I/O 시간 소모를 줄이고, 전체적인 실행 시간을 단축하였다. 이 방법은 특히 입력 데이터가 많은 경우에 유리하다.